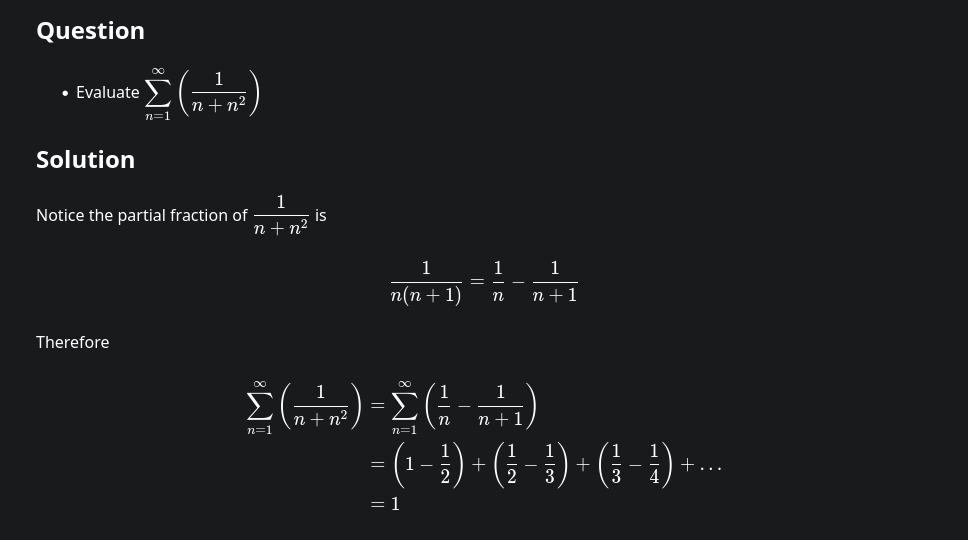• Evaluate SUM(1/(n + n^2)) from n = 1 to infty
  • WhoresonWells@lemmy.basedcount.comEnglish
    4·
    2 months ago

    Since this is everyone’s favorite example of telescoping sums, let’s do it another way just for giggles.

    Combinatorial proof

    The denominator is P(n+1, 2) which is the number of ways for 2 specified horses to finish 1st and second in an n+1 horse race. So imagine you’re racing against horses numbered {1, 2, 3, …}. Either you win, which has probability 0 in the limit, or there is a lowest numbered horse, n, that finishes ahead of you. The probability that you beat horses {1,2, … , n-1} but lose to n is (n-1)! / (n+1)! or P(n+1, 2) or 1/(n2+n), the nth term of the series. Summing these mutually exclusive cases exhausts all outcomes except the infinitesimal possibility that you win. Therefore the infinite sum is exactly 1.

  • zkfcfbzr@lemmy.world
    English
    4·
    2 months ago
    solution

    With partial fractions:

    1/(n + n²) = 1/(n(n+1)) = A/n + B/(n+1)

    A(n+1) + Bn = 1

    n = 0 gives A = 1, n = -1 gives B = -1

    1/(n+n²) = 1/n - 1/(n+1)

    Σ (n = 1 to ∞) 1/(n+n²) = Σ (n = 1 to ∞) 1/n - Σ (n = 1 to ∞) 1/(n+1)

    = Σ (n = 1 to ∞) 1/n - Σ (n = 2 to ∞) 1/n

    = 1/1 + Σ (n = 2 to ∞) 1/n - Σ (n = 2 to ∞) 1/n

    = 1

    Guessing this is the standard solution