I considered deleting the post, but this seems more cowardly than just admitting I was wrong. But TIL something!
I got tired of reading people saying that the infinite stack of hundreds is more money, so get this :
Both infinites are countable infinites, thus you can make a bijection between the 2 sets (this is literally the definition of same size sets). Now use the 1 dollar bills to make stacks of 100, you will have enough 1 bills to match the 100 bills with your 100 stacks of 1.
Both infinites are worth the same amount of money… Now paying anything with it, the 100 bills are probably more managable.
You could also just divide your infinite stack of $1 bills into 100 infinite stacks of $1 bills. And, obviously, an infinite stack of $100 bills is equivalent to 100 infinite stacks of $1 bills.
(I know this is only slightly different than what you’re getting at, which is that infinitely many stacks of 100 $1 bills is equivalent to an infinite stack of $100 bills)
Now paying anything with it, the 100 bills are probably more managable.
I’d take the 1’s just because almost everywhere I spend money has signs saying they don’t take bills higher than $20.
Yup. Exactly this.
They can spend the same amount of money, but at any moment the one with 100s has more money. If you have 2 people each picking up 1 bill at the same rate at any singular moment the person picking up the 100s will have more money.
Since we’re talking about a material object like dollar bills and not a concept like money we have to take into consideration it’s utility and have to keep in mind the actual depositing and spending would be at any individual moment. The person with 100s would have a much easier/quicker time using the money therefore the 100s have more utility.
We’re definitely not talking about this like a material object at the same time, though. There’s no way for a single person to store and access an infinite pile of bills.
You can spend a 100 dollar bill faster than a 1 dollar bill, sure, but both stacks would have the same money in the bank.
Except you’re given an infinite amount of bills, not money in the bank. So even when moving the money to the bank you’d be able to access it quicker with the 100s
deleted by creator
deleted by creator
Alternatively for small brains like me:
Imagine you have an infinite amount of $1 bills are laid out in a line. Right next to it is a line of $100 bills.
As you go down the line, count how much money you have at any given point.
Which total is worth more?
Your example introduces the axis of time which is not in consideration when discussing infinity. You’re literally removing infinity from the equation by doing that because “at any given point” by definition is not infinity. Let’s say that point is 1 million bills down the line. Now you’re comparing 1,000,000 x 100 vs 1,000,000 x 1, nothing to do with infinity
Imagine the line of 1s is stacked like pages in books on a shelf, but the line of 100s is placed in a row so they’re only touching on the sides. You could probably fit a few hundred 1s in the space of one 100. Both lines still have infinite bills in them, but now as you go along, you’re seeing a lot more 1s at a time.
That’s the thing about infinities, you can squish and stretch them, and they’re still infinite.
This kind of thread is why I duck out of casual maths discussions as a maths PhD.
The two sets have the same value, that is the value of both sets is unbounded. The set of 100s approaches that value 100 times quicker than the set of singles. Completely intuitive to someone who’s taken first year undergraduate logic and calculus courses. Completely unintuitive to the lay person, and 100 lay people can come up with 100 different wrong conclusions based on incorrect rationalisations of the statement.
I’ve made an effort to just not participate since back when people were arguing Rick and Morty infinite universe bollocks. “Infinite universes means there are an infinite number of identical universes” really boils my blood.
It’s why I just say “algebra” when asked what I do. Even explaining my research (representation theory) to a tangentially related person, like a mathematical physicist, just ends in tedious non-discussion based on an incorrect framing of my work through their lens of understanding.
For what it’s worth, people actually taking the time to explain helped me see the error in my reasoning.
There’s no problem at all with not understanding something, and I’d go so far as to say it’s virtuous to seek understanding. I’m talking about a certain phenomenon that is overrepresented in STEM discussions, of untrained people (who’ve probably took some internet IQ test) thinking they can hash out the subject as a function of raw brainpower. The ceiling for “natural talent” alone is actually incredibly low in any technical subject.
There’s nothing wrong with meming on a subject you’re not familiar with, in fact it’s often really funny. It’s the armchair experts in the thread trying to “umm actually…” the memer when their “experience” is a YouTube video at best.
It’s the armchair experts in the thread trying to “umm actually…” the memer when their “experience” is a YouTube video at best.
And don’t you worry, that YouTuber with sketchy credibility and high production values has got an exclusive course just for you! Ugh. Lol
I don’t know why you see it as an error. It’s the format of the meme. The guy in the middle is right, the guy on the left is wrong. That’s just how this meme works. But the punchline in this meme format is the the guy on the right agrees with the wrong guy in an unexpected way. I’m with the guy on the right and no appeals to Schröder–Bernstein theorem is going to change my mind.
Yeah I sell cabinets and sometimes people are like “How much would a 24 inch cabinet cost?”
It could cost anything!
Then there are customers like “It’s the same if I just order them online right?” and I say “I wouldn’t recommend it. There’s a lot of little details to figure out and our systems can be error probe anyway…” then a month later I’m dealing with an angry customer who ordered their stuff online and is now mad at me for stuff going wrong.
The two sets have the same value, that is the value of both sets is unbounded. The set of 100s approaches that value 100 times quicker than the set of singles.
Hey. Sorry, I’m not at all a mathematician, so this is fascinating to me. Doesn’t this mean that, once the two sets have reached their value, the set of 100 dolar bills will weigh 100 times less (since both bills weigh the same, and there are 100 times fewer of one set than the other)?
If so, how does it reconcile with the fact that there should be the same number bills in the sets, therefore the same weight?
I like this comment. It reads like a mathematician making a fun troll based on comparing rates of convergence (well, divergence considering the sets are unbounded). If you’re not a mathematician, it’s actually a really insightful comment.
So the value of the two sets isn’t some inherent characteristic of the two sets. It is a function which we apply to the sets. Both sets are a collection of bills. To the set of singles we assign one value function: “let the value of this set be $1 times the number of bills in this set.” To the set of hundreds we assign a second value function: “let the value of this set be $100 times the number of bills in this set.”
Now, if we compare the value restricted to two finite subsets (set within a set) of the same size, the subset of hundreds is valued at 100 times the subset of singles.
Comparing the infinite set of bills with the infinite set of 100s, there is no such difference in values. Since the two sets have unbounded size (i.e. if we pick any number N no matter how large, the size of these sets is larger) then naturally, any positive value function applied to these sets yields an unbounded number, no mater how large the value function is on the hundreds “I decide by fiat that a hundred dollar bill is worth $1million” and how small the value function is on the singles “I decide by fiat that a single is worth one millionth of a cent.”
In overly simplified (and only slightly wrong) terms, it’s because the sizes of the sets are so incalculably large compared to any positive value function, that these numbers just get absorbed by the larger number without perceivably changing anything.
The weight question is actually really good. You’ve essentially stumbled upon a comparison tool which is comparing the rates of convergence. As I said previously, comparing the value of two finite subsets of bills of the same size, we see that the value of the subset of hundreds is 100 times that of the subset of singles. This is a repeatable phenomenon no matter what size of finite set we choose. By making a long list of set sizes and values “one single is worth $1, 2 singles are worth $2,…” we can define a series which we can actually use for comparison reasons. Note that the next term in the series of hundreds always increases at a rate of 100 times that of the series of singles. Using analysis techniques, we conclude that the set of hundreds is approaching its (unbounded) limit at 100 times the rate of the singles.
The reason we cannot make such comparisons for the unbounded sets is that they’re unbounded. What is the weight of an unbounded number of hundreds? What is the weight of an unbounded number of collections of 100x singles?
Is it possible for infinite numbers to be larger than others? Or are all infinite numbers equal?
Yes, there are infinities of larger magnitude. It’s not a simple intuitive comparison though. One might think “well there are twice as many whole numbers as even whole numbers, so the set of whole numbers is larger.” In fact they are the same size.
Two most commonly used in mathematics are countably infinite and uncountably infinite. A set is countably infinite if we can establish a one to one correspondence between the set of natural numbers (counting numbers) and that set. Examples are all whole numbers (divide by 2 if the natural number is even, add 1, divide by 2, and multiply by -1 if it’s odd) and rational numbers (this is more involved, basically you can get 2 copies of the natural numbers, associate each pair (a,b) to a rational number a/b then draw a snaking line through all the numbers to establish a correspondence with the natural numbers).
Uncountably infinite sets are just that, uncountable. It’s impossible to devise a logical and consistent way of saying “this is the first number in the set, this is the second,…) and somehow counting every single number in the set. The main example that someone would know is the real numbers, which contain all rational numbers and all irrational numbers including numbers such as e, π, Φ etc. which are not rational numbers but can either be described as solutions to rational algebraic equations (“what are the solutions to “x^2 - 2 = 0”) or as the limits of rational sequences.
Interestingly, the rational numbers are a dense subset within the real numbers. There’s some mathsy mumbo jumbo behind this statement, but a simplistic (and insufficient) argument is: pick 2 real numbers, then there exists a rational number between those two numbers. Still, despite the fact that the rationals are infinite, and dense within the reals, if it was possible to somehow place all the real numbers on a huge dartboard where every molecule of the dartboard is a number, then throwing a dart there is a 0% chance to hit a rational number and a 100% chance to hit an irrational number. This relies on more sophisticated maths techniques for measuring sets, but essentially the rationals are like a layer of inconsequential dust covering the real line.
There are different things which could be called “infinite numbers.” The one discussed in the other reply is “cardinal numbers” or “cardinalities,” which are “the sizes of sets.” This is the one that’s typically meant when it’s claimed that “some infinities are bigger than others,” because e.g. the set of natural numbers is smaller (in the sense of cardinality) than the set of real numbers.
Ordinal numbers are another. Whereas cardinals extend the notion of “how many” to the infinite scale, ordinals extend the notion of “sequence.” Just like a natural number always has a successor, an ordinal does too. We bridge the gap to infinity by defining an ordinal as e.g. “the set of ordinals preceding it.” So {} is the first one, called 0, and {{}} is the next one (1), and so on. The set of all finite ordinals (natural numbers) {{}, {{}}, …} = {0, 1, 2, 3, …} is an ordinal too, the first infinite one, called omega. And now clearly {omega} = omega + 1 is next.
Hyperreal numbers extend the real numbers rather than just the naturals, and their definition is a little more contrived. You can think of it as “the real numbers plus an infinite number omega,” with reasonable definitions for addition and multiplication and such, so that e.g. 1/omega is an infinitesimal (greater than zero but smaller than any positive real number). In this context, omega + 1 or 2 * omega are greater than omega.
Surreal numbers are yet another, extending both the real and hyperreal numbers (so by default the answer is “yes” here too).
The extended real numbers are just “the real numbers plus two formal symbols, “infinity” and “negative infinity”.” This lacks the rich algebraic structure of the hyperreals, but can be used to simplify expressions involving limits of real numbers. For example, in the extended reals, “infinity plus one is infinity” is a shorthand for the fact that “if a_n is a series approaching infinity as n -> infinity, then (a_n + 1) approaches infinity as n -> infinity.” In this context, there are no “different kinds of infinity.”
The list goes on, but generally, yes-- most things that are reasonably called “infinite numbers” have a concept of “larger infinities.”
once the two sets have reached their value
will weigh 100 times less
there should be the same number bills in the sets
The short answer is that none of these statements apply the way you think to infinite sets.
How would you even weigh an infinite number of dollar bills? You’d need an infinite number of assistants to load the dollar bills onto the scale for you, and months to actually do it!
I see what you did here…
So to paraphrase, the raging person in the middle is right? I’ll take your answer no questions asked.
In short, yes.
If we only consider the monetary value, both “briefs” have the same value. Otherwise if we incorporate utility theory with a concave bounded utility curve over the monetary value and factor in other terms such as ease of payments, or weight (of the drawn money) then the “worth” of the 100 dollar bills brief could be greater for some people. For me, the 1 dollar bills brief has more value since I’m considering a potential tax evasion prosecution. It would be very suspicious if I go around paying everything with 100 dollar bills, whereas there’s a limit on my daily spending with the other brief (how many dollars I can count out of the brief and then handle to the other person).
I admit the only time I’ve encountered the word utility as an algebraist is when I had to TA Linear Optimisation & Game Theory; it was in the sections of notes for the M level course that wasn’t examinable for the Bachelors students so I didn’t bother reading it. My knowledge caps out at equilibria of mixed strategies. It’s interesting to see that there’s some rigorous way of codifying user preference. I’ll have to read about it at some point.
deleted by creator
Correct me if I’m wrong, but isn’t it that a simple statement(this is more worth than the other) can’t be done, since it isn’t stated how big the infinities are(as example if the 1$ infinity is 100 times bigger they are worth the same).
Sorry if you’ve seen this already, as your comment has just come through. The two sets are the same size, this is clear. This is because they’re both countably infinite. There isn’t such a thing as different sizes of countably infinite sets. Logic that works for finite sets (“For any finite a and b, there are twice as many integers between a and b as there are even integers between a and b, thus the set of integers is twice the set of even integers”) simply does not work for infinite sets (“The set of all integers has the same size as the set of all even integers”).
So no, it isn’t due to lack of knowledge, as we know logically that the two sets have the exact same size.
OK thanks for your explanation.
They’re both countibly infinite thus the same, no?
Theoretically, yes. Functionally, no. When you go to pay for something with your infinite bills, would you rather pay with N number of 100 dollar bills or get your wheelbarrow to pay with 100N one dollar bills? The pile may be infinite, but your ability to access it is finite. Ergo, the “denser” pile is worth more.
If we’re adding real world hypotheticals you would be paying for your shit on card anyway. You just go to the bank with how ever many truck loads of $100 bills when ever you needed a top up. Secondly you wouldn’t be doing it yourself, you pay someone else to do it. Thirdly as soon as the government found out you effectively had a money printer they would put you in prison or disappear you to prevent you from collapsing their money system, not to mention the serial numbers on the notes would have to be fraudulent because they wouldn’t match up with mints. And finally any physical object with an infinite quantity would be the size of the universe, likely causing either black hole or destroying the universe and us along with it. So in closing what sounds like a great situation is probably worth any potential risk
Yeah, this is what it comes down to. In calculus, infinity doesn’t exist, you just approach it when you take the limit. You’ll approach it “quicker” with the 100 dollar bills, so to speak
You’re thinking of a different calculus problem in this case we are comparing the growth rate of
100*\infty vs \infty. In calculus, you cannot accelerate the growth of \infty. If you put\infty / \inftyyour answer will beundefined(you can double check with Wolfram), similarly, if you put100*\infty / \infty, you will also getundefined
To establish whether one set is of a larger cardinality, we try to establish a one-to-one correspondence between the members of the set.
For example, I have a very large dinner party and I don’t want to count up all the forks and spoons that I’ll need for the guests. So, instead of counting, everytime I place a fork on the table I also place a spoon. If I can match the two, they must be an equal number (whatever that number is).
So let’s start with one $1 bill. We’ll match it with one $100 bill. Let’s add a second $1 bill and match it with another $100 bill. Ad infinitum. For each $1 bill there is a corresponding $100 bill. So there is the same number of bills (the two infinite sets have the same cardinality).
You likely can see the point I’m making now; there are just as many $1 bills as there are $100 bills, but each $100 bill is worth more.
You could make an argument that infinite $100 bills are more valuable for their ease of use or convenience, but infinite $100 bills and infinite $1 bills are equivalent amounts of money. Don’t think of infinity as a number, it isn’t one, it’s infinity. You can map 1000 one dollar bills to every single 100 dollar bill and never run out, even in the limit, and therefore conclude (equally incorrectly) that the infinite $1 bills are worth more, because infinity isn’t a number. Uncountable infinities are bigger than countable ones, but every countable infinity is the same.
Another thing that seems unintuitive but might make the concept in general make more sense is that you cannot add or do any other arithmetic on infinity. Infinity + infinity =/= 2(infinity). It’s just infinity. 10 stacks of infinite bills are equivalent to one stack of infinite bills. You could add them all together; you don’t have any more than the original stack. You could divide each stack by any number, and you still have infinity in each divided stack. Infinity is not a number, you cannot do arithmetic on it.
100 stacks of infinite $1 bills are not more than one stack of infinite $1 bills, so neither is infinite $100 bills.
You can map 1000 one dollar bills to every single 100 dollar bill and never run out, even in the limit, and therefore conclude (equally incorrectly) that the infinite $1 bills are worth more, because infinity isn’t a number.
Yes, the mapping that you’re describing isn’t useful; but that doesn’t invalidate the simple test that we can do to prove that two infinite sets are the same. And the test is pretty intuitive in some cases. If for every fork there is a spoon, then they must be an equal number. And if for every positive whole number (e.g “2”) there is a negative whole number (e.g. “-2”), then the set of positive whole numbers and the set of negative whole numbers must be the same.
Another thing that seems unintuitive but might make the concept in general make more sense is that you cannot add or do any other arithmetic on infinity.
I agree with you that adding infinity to itself just gets you the same number. But now we’re starting to ask: just what is infinity? We could think of infinity as a collection of things or we could think of infinity like we do numbers (yes, I know infinity is not technically among the real numbers). In the latter sense we could have a negative infinity {-1…-2…-3…etc.} that is quantitatively “worth less” than a countable positive infinity. On the other hand, if we think of infinity as a collection of stuff, then you couldn’t have a negative infinity because you can’t have less than zero members in the set.
I’ll admit that I’m getting out of my depth here since I know this stuff from philosophical study rather than maths proper. As with anything, I’m happy to be proven wrong, but I’m quite sure about the 1-1 correspondence bit.
Your 1-1 relationship makes sense intuitively with a finite set but it breaks down with the mathematical concept of infinity. Here’s a good article explaining it, but DreamButt’s point of every set of countable infinite sets are equal holds true because you can map them. Take a set of all positive integers and a set of all positive, even integers. At first glance it seems like the second set is half as big right? But you can map them like this:
Set 1 | Set 2
1|2
2|4
3|6
4|8
5|10
6|12
If you added the numbers up on the two sets you would get 21 and 42 respectively. Set 2 isn’t bigger, the numbers just increased twice as fast because we had half as many to count. When you continue the series infinitely they’re the same size. The same applies for $1 vs $100 bills.
$1|$100
$2|$200
$3|$300
In this case the $1 bills are every integer while the $100 bills is the set of all 100’s instead of all even integers, but the same rule applies. Set two is increasing 100x faster but that’s because they’re skipping all the numbers in between.
I understand that both sets are equally infinite (same cardinality). And I do see the plausibility in your argument that, in each case, since there’s an infinite number of bills their value should be equally infinite. If your argument is correct, then I should revise my understanding of infinity. So maybe you can help me make sense of the following two examples.
First, the number of rational numbers between 0 and 1 is countably infinite. That is, we can establish a 1-1 correspondence between the infinite set of fractions between 0-1 and the infinite set of positive integers. So the number of numbers is the same. But clearly, if we add up all the infinite fractions between 0 and 1, they would add up to 1. Whereas, adding up the set of positive integers will get us infinity.
Second, there are equally many positive integers as there are negative integers. If we add up the positive integers we get positive infinity and if we add up all the negative integers we get negative infinity. Clearly, the positive is greater than the negative.
In these two cases, we see that a distinction needs to be made between the infinite number of members in the set and the value of each member. The same arguably applies in the case of the dollar bills.
EDIT: I see now that I was mistaken.
But clearly, if we add up all the infinite fractions between 0 and 1, they would add up to 1.
0.9 and 0.8 are in that set, so they would add up to at least 1.7. In fact if you give me any positive number I can give you a (finite!) set of (distinct) fractions less than 1 which sum to more than that number. In other words, the sum is infinite.
I meant to say that we can infinitely divide the numbers between 0 and 1 and then match each with an integer. But I realized that the former wouldn’t be rational numbers, they would be real numbers.
That aside, I see now that the original idea behind the meme was mistaken.
But clearly, if we add up all the infinite fractions between 0 and 1, they would add up to 1.
Um no? 3/4 + 5/6 > 1
If you mean the series 1/2 + 1/3 + 1/4 + … that also tends to infinity
I meant to say that we can infinitely divide the numbers between 0 and 1 and then match each with an integer. But I realized that the former wouldn’t be rational numbers, they would be real numbers.
That aside, I see now that the original idea behind the meme was mistaken.
I don’t see what you are trying to say. You can also match 200 $1 bills with each $100 bill. The correspondence does not need to be one-to-one.
You’re right that we don’t need to, but mathematicians can use this method to prove that two infinite sets are the same size. This is how we know that the infinite set of whole numbers is the same size as the infinite set of integers. We can also prove that the set of real numbers is larger than the set of whole numbers.

I’m not quite sure how else to explain it, so I’ll link a Numberphile video where they do the demonstration on paper: https://www.youtube.com/watch?v=elvOZm0d4H0&t=19s . Here you can see why it’s useful to try to establish this 1-1 correspondence. If you can’t do so, then the size of the two infinite sets are not equal.
We can also prove that the set of rational numbers is larger than the set of whole numbers.
The video shows that rational numbers (aka fractions) are countable (or listable). Did you mean real numbers?
Good catch, I’ll edit that sentence
but each $100 bill is worth more.
But the meme doesn’t talk about the value of each $100 bill; it talks about the value of the bills collectively.
I think you’re misunderstanding the math a bit here. Let me give an example.
If you took a list of all the natural numbers, and a list off all multiples of 100, then you’ll find they have a 1 to 1 correspondence.
Now you might think “Ok, that means if we add up all the multiples of 100, we’ll have a bigger infinity than if we add up all the natural numbers. See, because when we add 1 for natural numbers, we add 100 in the list of multiples of 100. The same goes for 2 and 200, 3 and 300, and so on.”
But then you’ll notice a problem. The list of natural numbers already contains every multiple of 100 within it. Therefore, the list of natural numbers should be bigger because you’re adding more numbers. So now paradoxically, both sets seem like they should be bigger than the other.The only resolution to this paradox is that both sets are exactly equal. I’m not smart enough to give a full mathematical proof of that, but hopefully that at least clears it up a bit.
Adding up 100 dollar bills infinitely and adding up 1 dollar bills infinitely is functionally exactly the same as adding up the natural numbers and all the multiples of 100.
The only way to have a larger infinity that I know of us to be uncountably infinite, because it is impossible to have a 1 to 1 correspondence of a countably infinite set, and an uncountably infinite set.
~~I was thinking that, bill for bill, the $100 bill will always be greater value. But I can see the plausibility in your argument that, when we’re counting both the value of the members of each set, the value of the $100 bill pile can always be found somewhere in the series of $1 bills. The latter will always “catch up” so to speak. But, if this line of reasoning is true, it should apply to other countably infinite sets as well. Consider the following two examples.
First, the number of rational numbers between 0 and 1 is countably infinite. That is, we can establish a 1-1 correspondence between the infinite set of fractions between 0-1 and the infinite set of positive integers. So the number of numbers is the same. But clearly, if we add up all the infinite fractions between 0 and 1, they would add up to 1. Whereas, adding up the set of positive integers will get us infinity.
Second, there are equally many positive integers as there are negative integers. There is a 1-1 correspondence such that the number of numbers is the same. However, if we add up the positive integers we get positive infinity and if we add up all the negative integers we get negative infinity. Clearly, the positive is quantitatively greater than the negative.
In these two cases, we see that a distinction needs to be made between the infinite number of members in the set and the value of each member. The same arguably applies in the case of the dollar bills.~~
EDIT: I see now that I was mistaken.
Ah but you see if you take into consideration it’s talking about bills and not money in an account you have to take into consideration the material reality. A person who receives more 100s would have an easier time depositing and spending the money therefore they have higher utility, therefore they are worth more than the 1s.
Sure they may have the same amount of numbers (and 1, 2,3… May even be larger because you’ll eventually repeat in the 1:1 examile) but in reality the one with the 100s will have an easier time using their objects (100 dollar bills) than the ones who pick the 1 dollar bills
Infinity is a concept that can’t be reached so it can’t be counted up fully. Its not a hard number so you can’t get a full value from it since there is always another number to reach. Therefore you only peak at ∞ in any individual moment. You can never actually count it.
If you’re responding to the part about countable infinity and uncountable infinity, it’s a bit of a misnomer, but it is the proper term.
Countably infinite is when you can pick any number in the set and know what comes next.
Uncountably infinite is when it’s physically impossible to do that, such as with a set of all irrational numbers. You can pick any number you want, but it’s impossible to count what came before or after it because you could just make the decimal even more precise, infinitely.
The bizarre thing about this property is that even if you paired every number in a uncountably infinite set (such as a set of all irrational numbers) with a countably infinite set (such as a set of all natural numbers) then no matter how you paired them, you would always find a number from the uncountably infinite set you forgot. Infinitely many in fact.
It’s often demonstrated by drawing up a chart of all rational numbers, and pairing each with an irrational number. Even if you did it perfectly, you could change the first digit of the irrational number paired with one, change the second digit of the irrational number paired with two, and so on. Once you were done, you’d put all the new digits together in order, and now you have a new number that appears nowhere on your infinite list.
It’ll be at least one digit off from every single number you have, because you just went through and changed those digits.Because of that property, uncountably infinite sets are often said to be larger than countably infinite sets. I suppose depending on your definition that’s true, but I think of it as just a different type of infinity.
Sure if you’re talking about a concept like money, but we’re talking about dollar bills and 100 dollar bills, physical objects. And if you’re talking about physical objects you have to consider material reality, if you’re choosing one or the other the 100 dollar bills are more convinient. Therefore they have more utility, which makes them have a higher value.
I agree. I’m just being a math nerd.
I was actually discussing this with my wife earlier and her position is that the 1 dollar bills are better because it’s tough to find somebody who’ll split a 100, and 100s don’t work in vending machines.
I thought the hundreds would be better because you could just deposit them in the bank and use your card, and banks often have limits on how many individual bills you can deposit at once, so hundreds are way better for that.
if you’re talking about physical objects you have to consider material reality
If you’re considering material reality then you can’t have an infinite amount of it.
That’s a concession of the premise, you obviously can’t have infinite anything, but if you could then the 100s would bring more utility
Nah. We’re taking the singles and hitting up the strip club boiii.
Only valid retort
You’re right that they’re the same size but you’re mistaken when you try to assign a total value to the stack. Consider breaking each $100 bill into 100 $1 bills. The value is the same, clearly. So for each pair, you have a $1 bill and a small stack of 100 $1 bills. Now combine all singles back together in an infinite stack. Then combine all stacks of 100 into an infinite stack.
And you know what? Both infinite stacks are identical. They have the same value.
each $100 bill is worth more.
But the creation of each additional bill devalues the currency. At some point the value of all this paper money is negative because it’s not worth keeping and storing. The point at which they cross from positive to negative value would give them zero value, and they’d be equal.
You likely can see the point I’m making now; there are just as many $1 bills as there are $100 bills, but each $100 bill is worth more.
But the monetary value of the bills in each stack still adds up to infinity for both. It’s like having an uncapped Internet connection at 56 KBit/s versus 100 MBit/s: You can download all the things with both, but that alone doesn’t make them equal.
The reason infinity $100 bills is more valuable than infinity $1 bills: it takes less effort to utilize the money.
Let’s say you want to buy a $275,000 Lamborghini. With $1 bills, you have to transport 275,000 notes to pay for it. That will take time and energy. With $100 bills, you have to transport 2750 notes. That’s 100x fewer, resulting in a more valuable use of time and energy.
Even if you had a magical wallet that weighed the same as a standard wallet and always a had bills of that type available to pull out when you reach in. It’s less energy to reach in a fewer number of times.
Let’s toss in the perspective of the person receiving the money, too. Wouldn’t you rather deal with 2750 notes over 275,000, if it meant the same monetary value? If you keep paying in ones, people will get annoyed. Being seen favorably has value.
Value is about more than money.
You couldn’t buy that car with either denomination since money would have zero value now… and also the universe would collapse in on itself… but mainly the zero value thing.
Money only has zero value if people wideluly know you have infinity money.
And even then, unless you’ve spent huge amounts you won’t meaningfully inflate the money supply.
They won’t know anything because they’d be dead after all space was filled with dollar bills
You could just have a magic wallet that always had a 100$ in it. Take 100$ out, another spawns. Basically a money printer
Matter appearing in your wallet would instantly collide and possibly fuse with the air and other things in your wallet likely causing an intense plasma burst as matter was created from nothing. The bill would vaporize and I suppose could kill you.
very nice! But very OT tho
deleted by creator
I think it would be easier to go to thebank now and then to exchange some of your $100 for lower value bills than to do the opposite.
Besides, if there are places that don’t take bills less than $20, there are a lot of places that aren’t going to let you pay with only $1 bills. I can’t imagine a car dealership letting you do that. Or if you want to buy a home, etc.
Neither is bigger. Even “∞ x ∞” is not bigger than “∞”. Classical mathematics sort of break down in the realm of infinity.
It was probably mentioned in other comments, but some infinities are “larger” than others. But yes, the product of the two with the same cardinal number will have the same
Yes, uncountably infinite sets are larger than countably infinite sets.
But these are both a countably infinite number of bills. They’re the same infinity.
I think quite some people heard of the concept of different kinds of infinity, but don’t know much about how these are defined. That’s why this meme should be inverted, as thinking the infinities described here are the same size is the intuitive answer when you either know nothing or quite something about the definition whereas knowing just a little bit can easily lead you to the wrong answer.
As the described in the wikipedia article in the top level comment, the thing that matters is whether you can construct a mapping (or more precisely, a bijection) from one set to the other. If so, the sets/infinities are of the same “size”.
Yeah, inverting it is a good idea, truly
Yeah, we can still however analyze the statement f(x)=100x$/1x$ lim(x->inf) and clearly come to the conclusion that as the number of bills x approaches infinity will be equal to 100.
However, limes exists as a tool to avoid infinities and this exact problem when using calculus for practical applications - and as such it doesn’t apply here.
What about lemons?
Mathematically speaking, they should be converted to lemonade.
Screw that! I’m the man who’s gonna burn your house down! With the lemons! I’m gonna get my engineers to invent a combustible lemon that burns your house down!
Depends on if there’s any lemon stealing whores around.
You’re the guy in the middle by the way.
So it’s basically just a form of NaN?
It’s (literally) +Inf
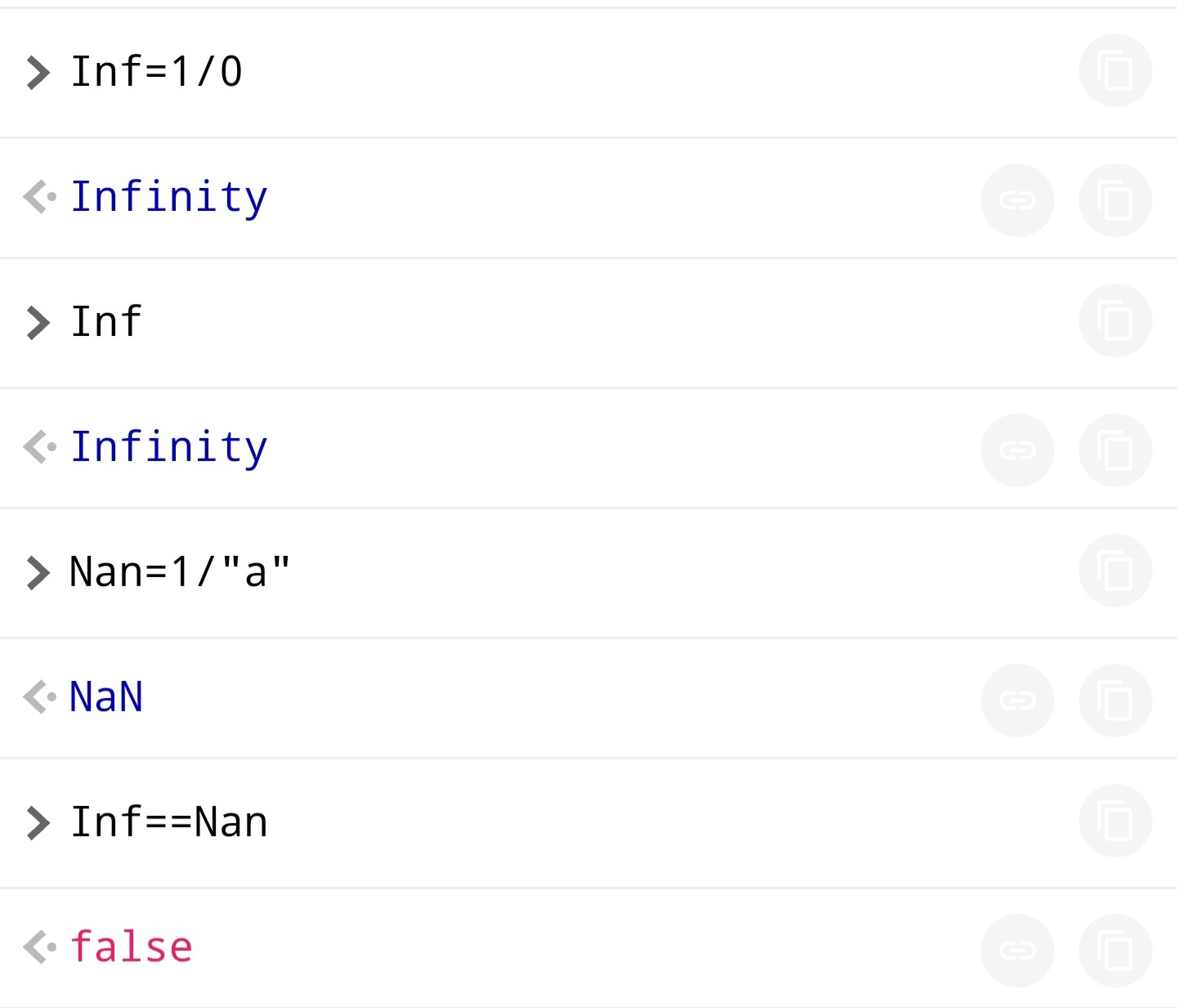
I didn’t know there was a special case for that. Neat.
This problem doesn’t involve cardinal numbers.
I considered deleting the post
Please don’t! I’ve been out and about today and inadvertently left this post open. I’ve thoroughly enjoyed reading all of the comments and it has been one of the most engaging posts I’ve seen on Lemmy
I appreciate all of the discussion it generated! Thank you <3
Duh, of course it is because it’s friggin hard to pay everything with 1 dollar bills, it will slowly eat away at your sanity.
Okay, I will pay you $100 for every 200 dollars you pick up out of this infinite pile and turn into $100 bills.
Now it won’t drive me insane at all, and you can get as rich as you want to be.
Infinity is not a number. Infinity is infinity.
People are confusing Infinity with lim x->Infinity. There’s a huge difference.
The hyperreals are a formal treatment of infinite numbers. It still doesn’t let people use infinity as a number in the way that posts like this suggest, but they’re interesting nonetheless. https://en.m.wikipedia.org/wiki/Hyperreal_number
There’s a huge difference.
Infinitely huge?
What does “worth” even mean in this set up?
I was just over here thinking this was about the practical utility of a $100 bill versus a wad of 100 $1 bills making an infinite quantity of the former preferable in comparison to (i.e. “worth more than”) the latter…
Removed by mod
nah aah, infinity plus 1 is more, I win
Infinity plus infinity … Na na NA NA na!!! I win! Na na NA NA na!!!
Infinity plus infinity, plus +1 to whatever anyone else says, recurring. No returns!!
I think you’ll find that’s sealed tight now and that I win. Na NAAAA!
/runs off maniacally
nonono, Infinity times infinity plus one, I win! *tehee nanana Na na na! *
No matter which denomination you choose, the infinite motel will always have room for another bill.
This is wrong. Having an infinite amount of something is like dividing by zero - you can’t. What you can have is something approach an infinite amount, and when it does, you can compare the rate of approach to infinity, which is what matters.
deleted by creator
Approaching an infinite amount of steel vs. Approaching an infinite amount of feathers.
Which weighs more?
An infinite amount of AeroGel.
Approaching infinite mass means you’ll probably form a black hole or end the universe before being able to weigh either of them
edit: meant to reply to the parent comment
Seriously though, infinity is Infinity, it’s not a number, it’s infinity.
Yes, the amount of both stacks is infinity. The question was not “What stack is easier to pay for something with”.
Both are equally easy to pay with since ∞ - X = ∞ if we disregard that 100s are more convenient way to pay for cars.
I bet you’ll get more questions buying a car with 100s than if you bought it with singles.
In Canada the $100 would be more convenient because we only gave $1 in coin form, which would be hella annoying to lug around.
Infinities can be different sizes (although in OPs case they are not): https://www.cantorsparadise.com/why-some-infinities-are-larger-than-others-fc26863b872f?gi=d5e83e23c757
Value is a weird concept. Even if mathematically the two stacks should have the same value, odds are some people will consider the $100 bill stack worth more, and be willing to do more in exchange for it. That effectively does make it worth more.
The moment you bring in the concept of actually using this money to pay for things, you have to consider stuff like how easy it is to carry around, and the 100s win. If your pile is infinite then you don’t even need 1s at the strip club.
An infinite stack of either would devalue the currency so as to be completely worthless. Well, perhaps worth whatever you can recycle those bills into.
Yes and no. If you spend that infinite money, then yes. The currency would be massively devalued as you would be adding money into the economy.
If you sat on it, nothing would happen. I imagine that the Federal Bank doesn’t know about your infinite stash and therefore isn’t taking into account any equation.
So, the value is inversely correlated to the ability to spend it.
… Still sounds worthless, TBH.
The money only devalues based on how much is in circulation. You’ll only devalue the currency as you spend it and you’d have to spend a trillion to have a non-minor effect.
If you manage to keep an infinitely large stack of bills a secret, sure. Once somebody notices and word gets out, I’m doubtful it doesn’t get devalued in a hurry. Since these are bills that we are assuming are valid, it’s going to seem like the central bank is printing money with abandon. Famously not great for public confidence in a currency. Why would I keep my wealth in a currency that somebody has an infinite amount of? They may not be spending it today, but who knows when that changes? I’d certainly be scrambling to convert mine to something else.